Der Kristallplanet: Ideengeschichte der globalen Gitternetze -

Teile die Wahrheit!

Globale Netze, Platonische Körper und die Musik der Erde: Strukturiert sich unsere Erde entsprechend dem Verlauf unsichtbarer, globaler Gitternetze? Gibt es Knotenpunkte innerhalb dieses Netzwerks von besonderer geologischer und geomantischer Bedeutung? Schwingt unsere Erde als ein großer Kristall? „Der Kristallplanet“ lädt dazu ein, über unser oft allzu materialistisches Bild von der Erde vor dem Hintergrund kosmischer Rhythmen und musikalischer Gesetzmäßigkeiten neu nachzudenken.

In der historischen Entwicklung der Globalgitter-Vorstellungen müssen zwei Hauptphasen unterschieden werden. Die erste Phase bilden die geologischen Hypothesen über eine kristalline Struktur der Erde in der Zeit von ca. 1850 bis 1920 – die russischen Arbeiten von Makarow, Morosow und Gontscharow aus den 70er-Jahren haben nämlich eine lange Vorgeschichte; sie, wie auch das Konzept von Schmutz, haben ihre Vorläufer in der Geologie des 19. Jahrhunderts, wie ich zeigen möchte.

Die große Wende in der Geschichte der Globalgitter-Vorstellungen markiert dann der berühmte Aufsatz von Christopher Bird im „New Age Journal“ von 1975, der ihre Verwandlung in eine New-Age-Idee einleitete. Bird griff drei russische Zeitschriftenartikel aus den Jahren 1973 auf und verband sie mit den Ideen von Ivan Sanderson aus der 2. Hälfte der 60er-Jahre, die sich im Zusammenhang mit den Forschungen zum „Bermuda-Dreieck“ entwickelt hatten. Die zweite Phase schließlich besteht in der Entwicklung der Globalgitter unter dem Einfluss von New-Age-Ideen, wobei diese sich mit den Vorstellungen der radiästhetischen Gitternetze und der Leylinien vermischten und zu „Energielinien“ wurden. In dieser Phase kamen auch die geometrischen Konzepte Buckminster Fullers und seines Fortsetzers Keith Critchlow ins Spiel. Diese Entwicklungsphasen werden im Folgenden in ihrer chronologischen Abfolge dargestellt. Durch genaue bibliographische Informationen zu allen besprochenen und zitierten Werken können alle Angaben vom interessierten Leser selbst überprüft werden.

Konzepte des 19. Jahrhunderts

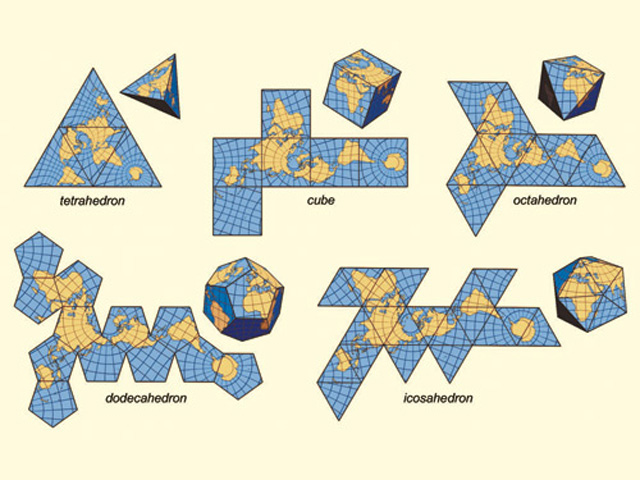
Die Idee, dass die Erde eine geometrische Gestalt besitzt, geht wohl auf die altgriechische Schule der Pythagoräer zurück. Wie die Russen und Bird anführen, findet sich bei Plato, der in vielem aus dieser Denkschule schöpfte, der Ausspruch, „von oben gesehen gleicht die Erde einem Ball aus zwölf Lederstücken“ (Phaidon 109A-110D). Plato bezieht sich bei diesem Vergleich auf den Ball, den Aphrodite dem Eros schenkte, damit er mit ihm Jason in Medea verliebt machen könne (Deonna, 1954; Le Roux, 1955). Gleichzeitig ist die Stelle ein Hinweis auf das Dodekaeder, einen der fünf „platonischen Körper“; die Lehre von den platonischen Körpern hatte Plato vermutlich ebenfalls von den Pythagoräern übernommen. Wie ich noch ausführen werde, spielt sie in den verschiedenen Konzepten der globalen Gitter immer wieder eine Rolle. Stark beeinflusst von platonischen Vorstellungen war auch der bedeutendste Naturforscher der beginnenden Neuzeit, Johannes Kepler (1571-1630). Er brachte 1596 in seinem ersten Buch „Mysterium Cosmographicum“ die von Kopernikus postulierten kreisförmigen (und von ihm selbst später als elliptisch erkannten) Planetenbahnen um die Sonne mit den fünf platonischen Körpern in Zusammenhang. In seiner „Weltharmonie“ (1619) hob er deren Bedeutung für das Verständnis der Erde hervor.

In der Geschichte der Geologie finden sich bereits im frühen 19. Jahrhundert eine ganze Reihe von Theorien, die bestrebt waren, die Gestalt der Erde, die Verteilung der Landmassen und die Struktur der Erdoberfläche kristallographisch zu erklären, so bei Delamotherie, Jameson, Oken und Hauslab. Etwas bekannter ist der Versuch des französischen Geologen Léonce Élie de Beaumont (1798-1874), Professor an der Pariser Ecole des Mines und am Collège de France sowie Generalinspektor der französischen Minen, Mitte des 19. Jahrhunderts die Struktur eines Dodekaeders in der Erdkruste zu sehen (Élie de Beaumont, 1847, 1849, 1850, 1852; Zittel, 1899). Beaumonts Ausgangspunkt war die Beobachtung, dass die Gebirgssysteme der Erde jeweils auf einem Kreis liegen; die einander überlappenden Kreise der verschiedenen Gebirgssysteme schneiden einander unter ganz bestimmten Winkeln. Élie de Beaumont schloss aus diesen Beobachtungen, dass die Verteilung der Gebirge auf der Oberfläche der Erdkugel nicht zufällig sei, sondern einem bestimmten Muster folgen müsse. Auf der Suche nach diesem Muster ging er von der Tatsache aus, dass die Oberfläche einer Kugel mit Hilfe von 15 Kreisen, von denen sich jeweils fünf in 12 Punkten unter einem Winkel von 36° schneiden, gleichzeitig in 20 gleichseitige Dreiecke wie auch in 12 regelmäßige sphärische Fünfecke aufgeteilt werden kann.

Die erste Aufteilung ergibt ein so genanntes sphärisches Ikosaeder, die letztere ein sphärisches Dodekaeder – zwei der fünf platonischen Körper; die drei anderen sind das Tetraeder, das Oktaeder und der Würfel. Mit anderen Worten, diese 15 Kreise teilen die Kugeloberfläche in 120 gleich große, rechtwinklige Dreiecke, welche nach Belieben entweder zu 30 Rauten, 20 gleichseitigen Dreiecken oder 12 regelmäßigen sphärischen Fünfecken (Pentagonen) zusammengefügt werden können. Da Élie de Beaumont Gründe zur Annahme hatte, dass in geologischen Zusammenhängen das Fünfeck von größter Bedeutung war, ging er davon aus, das gesuchte globale Muster in der Anordnung der Gebirgssysteme könnte ein Réseau pentagonal (pentagonales Netzgitter) mit zwölf fünfeckigen „Maschen“ sein. Die 15 Kreise entsprechen den Kanten eines im Mittelpunkt der Erde befindlichen regulären Ikosaeders – daraus konstruierte er das Pentagonalnetz als Basis der Anordnung der Gebirgssysteme.

Der französische Geologe schrieb in seinem Akademieaufsatz „Notes sur la corrélation des directions des différents systèmes de montagnes“ (1850), es sei vorstellbar, dass ein solches Muster durch die Kontraktion des Planeten entstanden sei, die dieser im Zuge seiner zunehmenden Abkühlung im Laufe der Jahrtausende durchgemacht habe. Man könne sich die Wirkungen dieser Kontraktion auf die Erdkruste in Analogie zur Bildung der hexagonalen Basaltsäulen vorstellen. Während aber bei der Teilung einer Fläche in gleiche Elemente gleichseitige Dreiecke, Quadrate oder Sechsecke entstehen könnten, wobei das Sechseck jene Fläche mit der größten Zahl von Seiten und dem geringsten Umfang darstellt, sei die Kugeloberfläche weder in regelmäßige Sechsecke noch in Quadrate, sondern nur in gleichseitige Dreiecke oder regelmäßige Fünfecke teilbar. „Die 15 Kreise, die die Kugeloberfläche in 12 regelmäßige Fünfecke teilen … bilden ein System von Linien mit dem flachsten Bogenmaß“ (es handelt sich also um so genannte Großkreise). Weiter heißt es bei Élie de Beaumont: „Wären die Auffaltungen der Erdkruste alle zur gleichen Zeit erfolgt, so wären vielleicht nur die 15 Kreise entstanden; da aber die Entstehung der verschiedenen Gebirgssysteme eine sukzessive war, so entstanden neben den pentagonalen zusätzlich auch oktaedrische, dodekaedrische und andere Kreise als notwendige Zwischenstufen im Übergang von dem einen zum nächsten der Grundkreise. Alle zusammen bilden sie gewissermaßen so etwas wie ein Klavier, auf dem die unermüdliche Natur, seit Beginn der Abkühlung des Planeten, eine Art von âJahrtausend-Harmonie entfaltet“. Dies zeigt, wie sehr Élie de Beaumont noch in der Tradition der idealistischen Morphologie stand, die mit ihrem harmonikalen Denken, der Tendenz von Goethes naturwissenschaftlichen Arbeiten nicht unähnlich, in der französischen Biologie und Naturphilosophie des 18. und frühen 19. Jahrhunderts (so bei Georges Cuvier und Geoffroy de St-Hilaire) eine zentrale Rolle spielte.

Kritik am pentagonalen Netzgitter

Da nicht alle bekannten Gebirgssysteme in das pentagonale Netz passten, musste Élie de Beaumont durch Berechnungen weitere subsidiäre Kreise zu Hilfe nehmen, die er aufgrund geometrisch-kristallographischer Voraussetzungen auswählte. Die komplexe Netzstruktur, die sich auf diese Weise ergab, veranlasste ihn dazu, die Erde als ein komplexes kristallines System von hoher Regularität zu betrachten, dessen Seiten sowohl von Achtecken, wie auch von Rhomben und Pentagonen, sowie von Trapezoiden und anderen Flächen gebildet wurden. Er hatte keine Schwierigkeiten, viele verblüffende Übereinstimmungen zwischen wichtigen geographischen Linien und seinem Netzgitter zu finden. Doch ist es, wie der Münchner Paläontologe Edgar Dacqué (1878-1945) im letzten Bericht der wissenschaftlichen Literatur, die wir über diese Vorstellungen des 19. Jahrhunderts haben, kritisch anmerkt, „von vornherein selbstverständlich, dass bei jedem nur einigermaßen engen Netz, das man über das endlose Mosaik tektonisch und morphologisch ganz heterogener und ihrer Struktur nach ganz grundverschiedener Schollen ausbreitet, aus denen die Erdoberfläche besteht, zahllose Punkte auf die Linien, in die Schnittpunkte und in die Zwischenräume dieses Netzes fallen“, ohne dass damit ein Beweis für irgendwelche Gesetzmäßigkeiten in der Anordnung der Mosaikstückchen und in dem Verlauf ihrer Grenzen erbracht wäre (Dacqué, 1915). In seinem Lehrbuch über die „Grundlagen und Methoden der Paläogeographie“ schreibt Dacqué, dass alle derartigen Versuche, gesetzmäßig verlaufende Linien in der Erdkruste nachzuweisen, abzulehnen seien, außer in dem Falle, dass sie durch bestimmte physikalische (geologische) Notwendigkeiten und Möglichkeiten nahegelegt würden. Dies schien ihm bei der sogenannten „Tetraedertheorie“ eher der Fall zu sein.

Frühe Tetraeder-Theorien

300x250

Auch Hans-Ulrich Schmutz „Tetraeder-Theorie der Erde“ (1986) hat nämlich ihre Vorläufer in der Geologie des 19. Jahrhunderts. Élie de Beaumonts Theorie, die außerhalb Frankreichs keine Anerkennung fand und nach seinem Tod rasch in Vergessenheit geriet, veranlasste den englischen Geologen William Lowthian Green 1857 zur Hypothese, die Erde dürfe nicht als Dodekaeder, sondern müsse als Tetraeder betrachtet werden. Das Tetraeder ist jener platonische Körper, dessen Flächen aus vier gleichgroßen Dreiecken gebildet werden und der sechs Kanten und 4 Ecken besitzt. Wenn man ein Tetraeder mit gleichem Volumen wie eine Kugel in diese einzeichnet, dann erhält man eine Figur, in der die vier Ecken über die Kugeloberfläche hinausragen; die Flächen befinden sich hingegen größtenteils innerhalb der Kugel. Kanten und Ecken liegen dann den Flächen gegenüber. Greens Tetraedertheorie, erst nicht beachtet, wurde später aufgegriffen und modifiziert vom Franzosen Albert Félix de Lapparent (1900) und ausgebaut vom Franzosen Marcel Bertrand (1900 a, b), den Engländern J.W. Gregory (1899, 1901) und Emerson (1900) sowie dem Deutschen Theodor Arldt (1905, 1907). Diese Geologen schlugen vor, die Erde als Tetraeder mit der Spitze am Südpol zu betrachten. Gregory wies darauf hin, dass in Élie de Beaumonts Netzgittermodell die antipodischen (einander auf entgegengesetzten Seiten der Erdkugel gegenüberliegenden) Gebiete immer eine ähnliche Struktur haben müssten, doch eine der fundamentalen Tatsachen der Geologie sei gerade die Unähnlichkeit der gegenüberliegenden Gebiete.

Argumente zur Tetraeder-Struktur

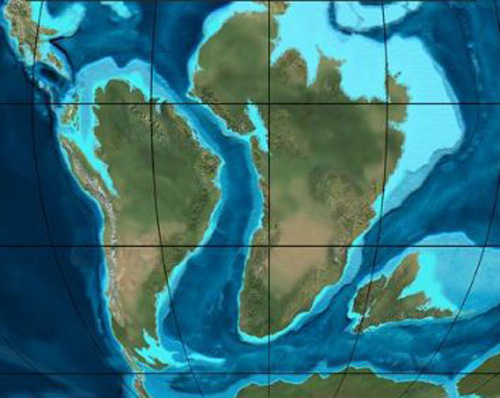
Die Tetraedertheorie würde erklären, warum Meere und Festlandschollen (mit Ausnahme einiger Teile von Südamerika) antipodisch liegen – der Landhalbkugel gegenüber liegt die Wasserhalbkugel, dem Nordpolarmeer gegenüber liegt die antarktische Landmasse. Für die Tetraedertheorie sprechen außerdem eine ganze Reihe von weiteren geologischen Tatsachen; wie Dacqué schreibt, kann sie deshalb nicht, wie die Beaumont-Theorie, einfach abgewiesen werden. Wenn die Spitze des Tetraeders durch den Südpol geht, dann muss am Nordpol eine der Flächen des Tetraeders liegen. Tatsächlich ist am Nordpol ein tiefes Meer von einem im Wesentlichen geschlossenen Landring umgeben. Wo die Ecken des Tetraeders vorstehen, würde man nach dem Tetraedermodell die stabilen Fixpunkte der Kontinentalmassen erwarten. Dies ist tatsächlich der Fall: die drei archaischen Urmassive des kanadischen Schildes, der den Norden der USA, Ost- und Mittelkanada sowie den größten Teil der nördlich davon gelegenen Regionen und den südlichen Teil Westgrönlands, mit der Hudson-Bay als Zentrum, umfasst, des finnoskandinavischen Schildes (Skandinavien, Finnland und der südlich anschließende Teil Russlands) und des ostsibirischen Schildes (das Angaramassiv und die Region zwischen den Flüssen Jenissei und Lena bis zum Baikalsee) – ihre Zentren liegen alle fast auf demselben Breitengrad – haben während der gesamten Erdgeschichte eine große Stabilität gegenüber Faltungsvorgängen bewahrt, was man von den Ecken eines solchen Erdtetraeders erwarten würde. Die vom nördlichen Landring ausgehenden, nach Süden zugespitzten Festlandsgrenzen Südamerikas, Afrikas und Australasiens, die entlang der meridionalen Kanten verlaufen und die Dreiecksgestalt der Kontinente ausmachen, entsprechen der nach Süden sich verjüngenden Spitze des Tetraeders. Auch der südliche Ozeangürtel, der einen südpolaren Kontinent umgibt, entspricht der Erwartung des Modells. Ebenso passt die bisher nicht erklärte unterschiedliche Abplattung der beiden Polargebiete – der Nordpol ist stärker abgeplattet als der Südpol – ins Tetraedermodell. Messungen des Gravitationsfeldes der Erde an den Orten von zweien der hypothetischen Tetraederecken (Nordamerika und Wolgabecken) ergeben ein Schwerefeld, das für eine kugelförmige Erde zu gering, aber mit der Annahme einer tetraederförmigen Erde vereinbar ist.

Theorie zur Kontraktion der Erdkruste

300x250 boxone

Die Autoren der Tetraedertheorie nehmen, wie Élie de Beaumont, an, dass die Tetraederform durch die Kontraktion bei der Abkühlung der Erdkruste entstanden sei. Arldt argumentiert, die tetraedrische Form sei diejenige, die die tangentialen Spannungen am besten ausgleiche. Unter allen regelmäßigen Körpern mit gleicher Oberfläche sei das Tetraeder derjenige mit dem kleinsten Volumen. Wenn das Volumen einer Kugel abnimmt, ohne dass gleichzeitig die Oberfläche entsprechend damit Schritt halten kann, so verwandelt sich die Kugel nach Möglichkeit in ein Tetraeder, weil diese Form ihr am längsten die Erhaltung ihrer früheren Oberfläche erlaubt. Nach Green ist auch die 23,5°-Abweichung der Erdachse von einer ursprünglich senkrechten Lage auf die Bildung des Tetraeders zurückzuführen, da sich dabei ein Massenüberschuss nördlich des Äquators ergab. Gleichzeitig habe dies infolge der Anziehung von Sonne und Mond die Erscheinungen der Präzession und der Nutation hervorgerufen, unter deren Einfluss sich die erwähnte Neigung der Erdachse im Laufe des Jahres geringfügig verschiebt.
Dacqué hielt die Tetraeder-Hypothese insgesamt für plausibel, wies jedoch darauf hin, dass die „zweifellos vorhandene tetraedrische Verteilung der Landmassen und Meere“ nicht bei der Erkaltung des Planeten entstanden sein könne, sondern jüngeren Datums sein müsse, weil ja diese Form aus der heutigen Struktur der Erdoberfläche erschlossen worden sei. Bei einer frühen erdgeschichtlichen Bildung wären diese Strukturen infolge der diversen Umgestaltungsprozesse kaum mehr vorhanden.

Die Tetraedertheorie von Schmutz

Der Schweizer Hans-Ulrich Schmutz schließlich, Geologe und Lehrer an der Waldorfschule Wetzikon bei Zürich, der in seinem Werk „Die Tetraederstruktur der Erde“ (1986) die bisher jüngste Version dieser Vorstellung von der kristallinen Struktur unseres Planeten vorgelegt hat, scheint nichts von diesen Vorläufern zu wissen. Er zitiert keinen der erwähnten Autoren und geht einzig von einigen Anregungen von Rudolf Steiner (1861-1925) aus den 20er-Jahren über die Kreuzstruktur der globalen Gebirgszüge und die Tetraederstruktur der Erde aus. Der Gründer der Anthroposophie selbst kannte aber vermutlich zumindest Dacqués Veröffentlichung, denn beide waren Mitglieder der Theosophischen Gesellschaft, und Dacqués naturphilosophische Arbeiten waren Steiner mit Sicherheit bekannt. Steiner hatte 1920 in den Lehrplanangaben für die Waldorfschulen die Lehrer aufgefordert, die Struktur der Gebirge rund um die Erde als zwei kreuzförmig aufeinander stehende Ringe anschaulich zu machen. Im Anschluss an einen Vortrag zur Entstehung der Vulkane entwickelte Steiner dann 1924 seine Vorstellungen zur Tetraederstruktur der Erde. In seinem Buch unternahm es Schmutz, die seit Steiners Hinweisen (und seit den oben beschriebenen früheren Tetraedertheorien) gemachten Erkenntnisfortschritte der Geologie auf ihre Verträglichkeit mit der Tetraedertheorie zu überprüfen.

Aspekte der Plattentektonik

Durch die Erkenntnisse der „Kontinentalverschiebungstheorie“, die hauptsächlich der deutsche Geophysiker Alfred Wegener (1880-1930) ab 1912 entwickelte und 1915 in seinem Buch „Die Entstehung der Kontinente und Ozeane“ darstellte, wurde die Geologie auf eine völlig neue Grundlage gestellt; seinen vorläufigen Abschluss erhielt dieser Prozess durch das in den 70er-Jahren von J.T. Wilson und anderen entwickelte Konzept der „globalen Plattentektonik“, das Gebirgsbildung, Vulkanismus und Erdbebenzonen in einen inneren Zusammenhang brachte. Die den Tetraedertheoretikern des 19. Jahrhunderts noch verborgenen Bewegungsvorgänge innerhalb der Erdkruste sind – nach der Entdeckung des „Mittelozeanischen Rückens“, eines untermeerischen Gebirges, das sich durchgehend über eine Länge von 70000 Kilometer mitten durch den Atlantik, den Indischen Ozean und den Südpazifik hinzieht, und der weltweiten systematischen Bestandesaufnahme eines Teils der kontinentalen Erdkruste – heute im Großen und Ganzen bekannt.

Nach den Erkenntnissen der Plattentektonik besteht die Erdkruste aus einer Anzahl von so genannten Platten, die sich mit verschiedenen Bewegungsrichtungen aufeinander zu oder voneinander weg bewegen. An den Plattengrenzen gibt es somit einerseits „Ausdehnungszonen“, andererseits „Kompressionszonen“. Die Erdkruste durchläuft auf der einen Seite einen Prozess kontinuierlicher Ausdehnung, der vor allem im Bereich der erwähnten untermeerischen Gebirgsrücken, aber auch in einigen kontinentalen Dehnungszonen wie dem ostafrikanischen Grabenbruchsystem (Rotes Meer, Jordantal), im Golf von Kalifornien (mit dem berüchtigten San-Andreas-Graben) und im Grabenbruch des sibirischen Baikalsees vor sich geht. Auf der anderen Seite findet gleichzeitig in den Kompressionszonen ein Prozess der Krustenverkürzung statt, so beispielsweise in den Alpen und im Himalaya. Interessant ist, dass dem erwähnten weltumspannenden untermeerischen Gebirgsrücken der Dehnungszonen ein etwa gleich langer Gürtel von jungen Faltengebirgen und Inselgebirgen gegenübersteht, in deren Region mit der Auffaltung der Gebirge eine Zusammenziehung der Erdkruste stattfindet.

Diese von Schmutz entdeckte Polarität von submarinen Dehnungszonen und kontinentalen Kompressionszonen zeigt sich auch, wenn man das Gefüge der Dehnungs- und Kompressionslinien an den Plattengrenzen auf ihre Geometrie untersucht. Die Ausdehnungslinien teilen nämlich die Erdoberfläche in vier Felder, von denen sich jeweils drei an vier Stellen (den „Tripelpunkten“) treffen, nämlich in Ostsibirien (N in obiger Grafik), bei den Bouvet-Inseln im Südatlantik (A), bei der Insel Rodrigues im Indischen Ozean (I), und bei den Osterinseln im Pazifik (P). Die Feldgrenzen werden durch die Mittelozeanischen Dehnungsrücken, die kontinentalen Riftzonen der großen Bruch- und Grabensysteme und die seismisch schwach aktiven, basischen Vulkane markiert. Eine zweite Einteilung der Erdkruste in vier Felder ergibt sich aus den Kompressionslinien, wobei die Linien des Zusammenschubs der Erdkruste – die erdgeschichtlich jungen kontinentalen Faltungszonen und Tiefseegräben – sowie die Zonen intensiver Erdbebentätigkeit und seismisch stark aktiver, saurer Vulkane die Feldgrenzen bilden. Hier sind Honduras (H), der Kaukasus (K), Japan (J) und die Gegend des Südpols (S) die Tripelpunkte.

Argumente zur Oktaeder-Struktur

Beide Male ergibt sich ein Gebilde mit vier Ecken, vier Flächen und 6 Kanten – mit anderen Worten, ein Tetraeder, das man sich hier als sphärisch abgerundetes Tetraeder mit gebogenen Dreiecksflächen und einem teilweise stark verbogenen Verlauf der Kanten vorstellen muss. Bei Berücksichtigung der zwei Typen von Vulkanen als Kantenlinien bekommt man somit ein System von zwei sich durchdringenden Tetraedern, einem Ausdehnungstetraeder mit vier Ecken südlich des Äquators (Honduras, Kaukasus, Japan und Südpol) und der Spitze am Südpol, und einem Kompressionstetraeder mit 3 Ecken nördlich des Äquators (Ostsibirien, Bouvet-Inseln, Rodrigues-Insel und Osterinseln) und der Spitze in Ostsibirien. Nach Schmutz ist das Kompressionstetraeder das geologisch ältere; im Laufe der erdgeschichtlichen Entwicklung sei durch Umwandlung von Mineralien im Erdmantel, was zur Ausdehnung der Erdkruste führte, das dazu polare Dilatationstetraeder entstanden. Als Folge dieser Polarität habe sich dann durch Kombination beider Tetraeder zusätzlich ein Oktaeder herausgebildet. Das Tetraeder ist nämlich der einzige platonische Körper, der eine Links- und eine Rechtsform aufweist, in sich also polar ist. Kombiniert man diese zwei polaren Formen, entsteht die höhersymmetrische Durchdringungsform des Oktaeders, jenes platonischen Körpers, der acht Flächen (gleichseitige Dreiecke), sechs Ecken und zwölf Kanten besitzt. Dabei werden jeweils die sechs Kreuzungsstellen des Kompressions- mit dem Dilatationstetraeder zu Ecken eines sphärisch gerundeten Oktaeders.

Das Gebirgskreuz

In einer Oktaederstruktur wäre auch das von Steiner erwähnte rechtwinklige Gebirgskreuz besser erklärbar als im Tetraedermodell. Es wird gebildet von zwei um den Erdball laufenden Gebirgsketten, in Nord-Süd-Richtung von der Kette, die von den Rocky Mountains und den Anden sowie ihrer Unterwasser-Fortsetzung auf der gegenüberliegenden Halbkugel gebildet wird, dem so genannten Ninety-East-Rücken, einem bedeutenden untermeerischen Gebirgszug im Indischen Ozean, dessen Verlängerung dann Indochina und die japanischen Inseln bilden. In West-Ost-Richtung ist es die die Gebirgskette, die mit den Alpen beginnt, über den Kaukasus und den Himalaya weiterläuft, sich über Burma, Thailand, Indonesien und Neuguinea fortsetzt und auf der anderen Seite des Globus untermeerisch über die „Wallace-Bruchzone“ in die so genannte Clipperton-Bruchzone (sie reicht von den Marquesa-Inseln im Ostpazifik bis nach Honduras) und schließlich über Kuba, Puerto Rico und den Atlantik wieder in die Alpen übergeht. Diese beiden Gebirgsringe schneiden sich rechtwinklig in Honduras und in Indochina.

Geomantisch besonders interessant ist, dass die Projektionen dieser beiden Kreuzungspunkte des globalen Gebirgskreuzes auf die jeweils gegenüberliegende Seite des Globus an zwei sehr bedeutsamen Stellen zu liegen kommen: die eine liegt im Colorado-Hochplateau im Vierländereck, in dem die nordamerikanischen Bundesstaaten Utah, Colorado, Arizona und New Mexico aneinander grenzen, die andere im südlichen Hochland von Tibet. Beide Regionen sind wichtige „Heilige Gebiete“, werden von den Hopi-Indianern und der tibetischen Kultur als polare Kraftpole der Erde betrachtet und besitzen eine Vielfalt von geologischen, geophysikalischen und meteorologischen Besonderheiten, worauf vor allem die amerikanische Künstlerin und Forscherin Joan Price hingewiesen hat (Price, 1979, 1985; Dömpke, 1982). Im Rahmen des Tetraedermodells muss man sich vorstellen, dass die rechtwinkligen Gebirgskreuze durch die Verformung des Kompressionstetraeders mit seinen ursprünglich kleineren Winkeln hervorgerufen wurden.

Erze lagern an Tetraederkanten

Ein weiterer bedeutsamer Zusammenhang, den Schmutz hergestellt hat, ist derjenige zwischen der Tetraederstruktur der Erde und der Lage der größten Metall-Lagerstätten und -Abbaugebiete auf der Erdoberfläche. Es scheint dabei auch einen Zusammenhang mit der Kristallisationsform der betreffenden Metalle zu geben. Bei dieser Verteilung spielt offenbar nur das jüngere Ausdehnungstetraeder eine Rolle, während das ältere Kompressionstetraeder nur indirekte Bedeutung hat. Da die ständige Bildung neuer Kruste in den Mittelozeanischen Rücken ein Absinken dieser Kruste an den Plattenrändern und Untertauchen unter die Nachbarplatten bewirkt, bilden sich die erdgeschichtlich jungen, in gediegener Form oktaedrisch-kubisch kristallisierenden Metallerze Gold, Silber und Kupfer an den Kanten des Kompressionstetraeders, vor allem auf der Nordhalbkugel. Das kubisch kristallisierende Silber ist, wenn es mit Gold zusammen auftritt, immer an die Tetraederkanten gebunden; auch das Gold der jungen Goldformationen und das an Andesit gebundene Kupfer wird vorwiegend dort gefunden.

Die alten Goldformationen und Kupfererze hingegen finden sich vorzugsweise im Zentrum von Tetraederdreiecken in Afrika und Europa, die polar zum zirkumpazifischen Gürtel liegen. In der Regel weiter entfernt von den Tetraederkanten, in Richtung der Mittelpunkte der Tetraederdreiecke liegen auch Blei-, Zinn- und Quecksilbervorkommen. Das kubisch kristallisierende Blei wird sowohl in der Nähe der Kanten (junge Bildungen) wie auch innerhalb des Tetraeders (alte Bildungen) auf der Nord-Halbkugel in Europa und Nordamerika gefunden. Das tetragonal kristallisierende Zinnerz hingegen ist ein Metall der Südhalbkugel, wo seine jungen Bildungen in Südostasien und den zentralen Anden und seine alten Formationen in den Dreiecken Honduras-Kaukasus-Südpol (Südamerika, Afrika) sowie Kaukasus-Japan-Südpol (Australien, Indonesien) gefunden werden, alle in Kantennähe. Die seltenen Fundstellen des Quecksilbers nehmen eine Zwischenstellung ein und sind in zwei kurzen Kantenabschnitten in Europa und Kalifornien, beide innerhalb des Dreiecks Honduras-Kaukasus-Japan, lokalisiert. Die Lagerstätten des Eisenerzes mit seiner Vielfalt der möglichen Kristallisationsformen schließlich nehmen mit ihrer flächigen Verteilung eine Sonderstellung ein. Jüngeres Erz findet sich an jenen Tetraederkanten, wo auch Kupfervorkommen sind. Älteres Erz ist auf den gesamten Flächen der Tetraederdreiecke Honduras-Kaukasus-Südpol und Honduras-Kaukasus-Japan zu finden.

Unregelmäßigkeiten der Erdkugel

In die Oktaederstruktur, die die Erdoberfläche in acht Dreiecke unterteilt, fügen sich nach Schmutzs Angaben auch eine Reihe geologischer und geophysikalischer Eigenschaften gut ein, darunter die eigenartige Unregelmäßigkeit des so genannten Geoids, die Anomalien des Erdmagnetfeldes, die Wärmeflussverteilung der Erde und die Konvektionsströmungen. Schon seit einigen Jahrzehnten weiß die Geologie, dass die Erde keine Kugel ist, sondern eher so etwas wie eine Birnenform besitzt und außerdem an vier Stellen gewissermaßen Höcker von etwa 70 Kilometer Höhe und an vier weiteren Stellen Dellen von rund 70 Kilometer Tiefe aufweist. Diese Geoid-Form der Erde weist eine verblüffende Übereinstimmung mit der Oktaederstruktur auf. Auch die Karte der jährlichen Abweichungen der magnetischen Kompassnadel vom geographischen Nordpol zeigt eine beinahe perfekte Übereinstimmung mit den auch beim Geoid gefundenen acht Feldern, wenn man die Gebiete mit einer Zunahme der Abweichung von jenen, die eine Abnahme aufweisen, trennt. Auf einer Karte der weltweiten Variation des Wärmeflusses stimmen die Gebiete mit stark erhöhtem Wärmefluss ungefähr mit den Höckern des Geoids, jene mit abgeschwächtem Wärmefluss mit den Dellen überein. Die weiter oben in anderem Zusammenhang bereits erwähnten Fließbewegungen des verflüssigten Gesteins im Erdmantel (Konvektionsströmungen) zeigen dieselbe achtkammerige Struktur auf der Erdoberfläche.

Die verschiedenen platonischen Körper, die Schmutz in der Struktur der Erdkruste zu sehen glaubt, sind nach seiner Auffassung Anzeichen für eine Metamorphose des Erdkörpers, die im Laufe der Erdgeschichte durch systemimmanente Gestaltkräfte bewirkt werden. Er sieht eine geometrische Entwicklung von der ursprünglichen Kugelform des noch nicht verfestigten „Erdkeims“ über die Tetraederstruktur bei der Bildung der festen Erde bis hin zur Bildung der heutigen orthogonalen Struktur mit dem Gebirgskreuz.

Teil 01, weitere folgen…

…
Buch: Der Kristallplanet: Globale Netze, Platonische Körper und die Musik der Erde. Von Marco Bischof. Euro 19,50. Veröffentlicht am: 2008-05-31
Abmessungen: 9.17″ h x .98″ b x 5.94″ l,
Einband: Broschiert
308 Seiten

Quelle: PublicDomain/Wikipedia/geomantie.net 07/2000

One thought on “Der Kristallplanet: Ideengeschichte der globalen Gitternetze”

Vic W Desotelle sagt:

29. Mai 2021 um 19:24 Uhr

Hello, I found you through Dan Winter’s work. I am looking for global maps and globes that are overlaid with the tetragrammaton and other sacred geometric configurations that show where the vector points touch the planet and could be used to study new forms of energy and/or communications systems through it. It seems this was already done in the ancient past. Now I seek to understand how it can be applied today. Do you have such 2D and 3D maps available for my study? Kind thank you for your work. Vic Desotelle

Antworten

Der Kristallplanet: Ideengeschichte der globalen Gitternetze

About aikos2309

One thought on “Der Kristallplanet: Ideengeschichte der globalen Gitternetze”

Schreibe einen Kommentar Antworten abbrechen

About aikos2309

One thought on “Der Kristallplanet: Ideengeschichte der globalen Gitternetze”

Schreibe einen Kommentar Antworten abbrechen

Entdecke mehr von